Lines, Planes & Geometry - Mathematics as Art
AA
The only way to understand any complex subject is to visualize it, imagine and re imagine the concepts as stories or a sequence of images. Mathematics is no exception, hence we use 'Geometry' as a tool to understand the Math needed for ML.
Equation of Hyper-plane:
Hence if there exists a vector "W" perpendicular to the plane "A" passing through Origin, then the product of any vector "X" on the plane "A" and the vector "W" is ZERO.
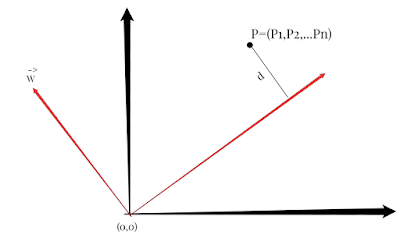
Suppose there is a vector "W" perpendicular to a plane passing through Origin and there exists a point P such that P=(P1,..Pn) then the distance "d" between P and the plane is:
Suppose there is a line "L" and a point (x0,y0) on the line with slope"m" then the equation of the line can be represented as:
Equation of Hyper-plane:
w0+w1x1+w2x2+…+wnxn=0
If the plane passes through ORIGIN, then w0=0 → WTX = 0
Hence if there exists a vector "W" perpendicular to the plane "A" passing through Origin, then the product of any vector "X" on the plane "A" and the vector "W" is ZERO.
Suppose there is a vector "W" perpendicular to a plane passing through Origin and there exists a point P such that P=(P1,..Pn) then the distance "d" between P and the plane is:
D = WTP / ||W||
Point Slope Form:
Suppose there is a line "L" and a point (x0,y0) on the line with slope"m" then the equation of the line can be represented as:
y-y0=m(x-x0)
Slope Intercept Form:
With the y-intercept b=(o,b), the line equation with slope 'm' and the y-intercept 'b' can be represented as:
y=mx+b
Tangetns/Instantaneous rate of change/Derivative:
Slope of a tangent is the 'rate of change' of F(x) at X=a. This is also called as the 'DERIVATIVE' of function at 'a'.
f|(a) = lim h->0
[f(a+h) – f(a)] / h ----- equation(1)
Geometric Proof:
Point(a,f(a) lies on the tangent. Th eslope of the line segment with points (a,f(a)) and (a+h,f(a+h)) is:
[f(a+h) - f(a)]/h
Now, if "h" were to get closer to "ZERO", then the slope of the line segment would be almost equal to the slope of the tangent. and hence the equation(1) is the slope of the tangent and is the instantaneous rate of change.



Comments
Post a Comment
Hey there, feel free to leave a comment.