Did you say Matrix?
Matrix: A rectangular array of numbers or equations arranged in rows and columns. The dimension of a matrix defines te structure of the matrix specifying the number of rows and columns in it.
Matrix 'A' shown above is a 2x2 matrix, meaning it has 2 rows and 2 columns. Each element of the matrix can be represented as:
A11 = a1
A12 = b1
A21 = c1
A22 = d1
Some of my cousins:
Square Matrix: Number of rows = Number of columns
Diagonal Matrix : A square matrix with all elements except diagonal elements are ZEROES
Identity Matrix : A diagonal matrix with "1"s as diagonal elements.
Addition:
As long as the dimensions of two matrices are same, the corresponding elements can be added.
Multiplication:
To multiply matrix A with dimensions nxm and matrix B with dimensions pxq, "m should be equal to p".
Transpose:
If we interchange the rows and columns of a matrix, the resultant matrix is the Transpose.
The following equations can be represented in matrix form as:
3x1+9x2+7x3=7
x1+4x3=11
8x2+x3=10
Linear Dependency:
If a columns can be expressed as a combination of any other columns of a matrix, it implies there is a Linear Dependency.
The column "c" can be expressed in terms of columns of a and b. Hnce there exists a linear dependency among the columns.
Rank of a Matrix:
The total number of LINEARLY INDEPENDENT columns of a matrix is the Rank of a matrix.
Rank(A) = 2
Why is determining the rank of a matrix important?
Unidentified linearly dependent columns contribute to higher VARIANCE in data. This can be avoided if we determine the rank of the matrix beforehand and club the linearly dependent columns before any analysis is even performed.
Determinant of a Matrix:
Inverse of a Matrix:
A * A-1 = I
An algebraic equation can be solved using the inverse matrix.
Since A.X = b → X = b. A-1
Note:
Inverse of a matrix be determined:
- Iff the determinant of the matrix is not ZERO or if there exists a ZERO in the diagonal elements.
- Iff the columns are linearly independent.
(AxB)-1 = B-1 x A-1
Eigen Values and Eigen Vectors:
For a nxn matrix 'A', a scalar 'λ' is called its EIGEN VALUE if ∃ a non-zero vector 'X' such that AX = λX. Such a vector is called as EIGEN VECTOR.
If λ is an eigen value of matrix A and X is the eigen vector of λ, any none-zero multiple of X will be an eigen vector.
Similarly, for a 3X3 matrix A, we can get the eigen values and the corresponding eigen vectors. The operation a bit complex though. |A-λI| = 0 can be solved as:
λ3-(Sum of the diagonal elements of A) λ2 +
(Sum of the diagonal minors of A) λ - |A|= 0
For each 'λ' we can get the corresponding eigen vector using the Crammer's Rule.





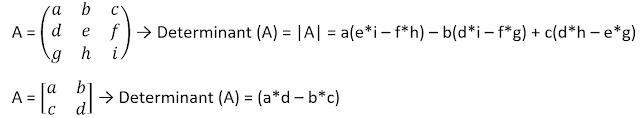



Comments
Post a Comment
Hey there, feel free to leave a comment.